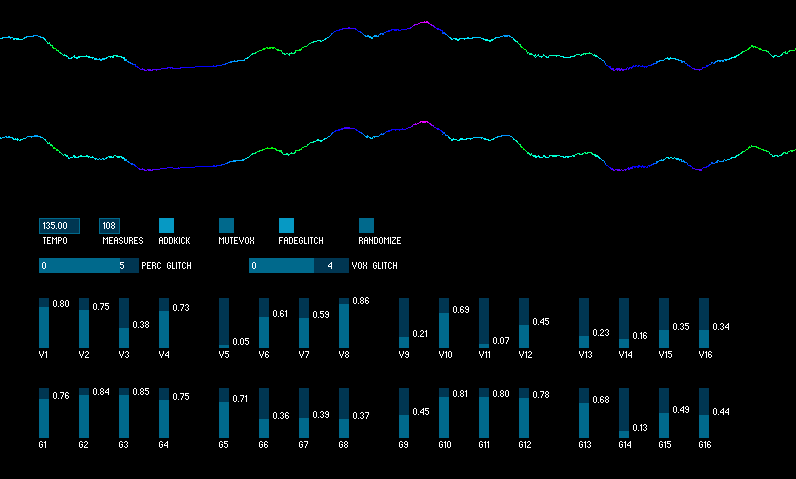
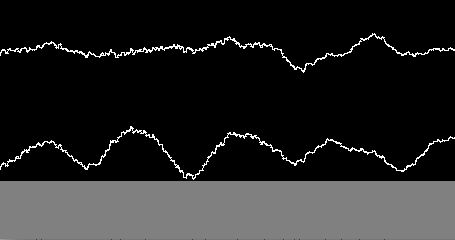
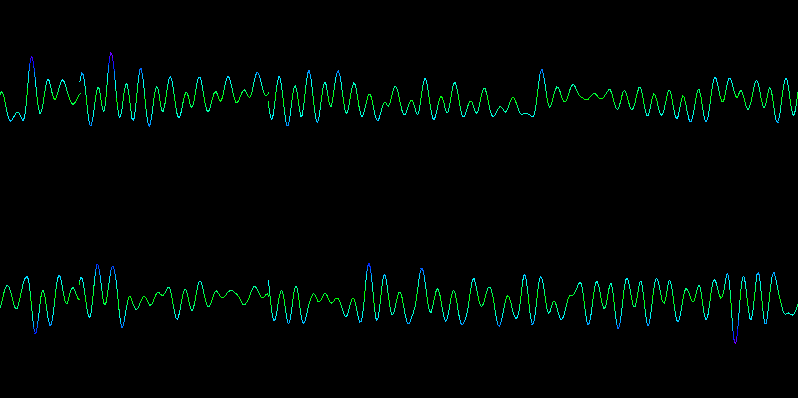
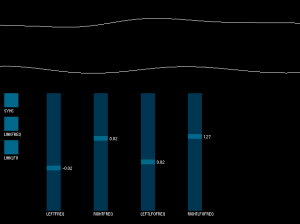
I’ve received several questions about the TickRate UGen that I’ve used in some recent Sound Bytes. Quite simply, this is a UGen that allows you specify an audio generation rate. Setting a rate of 1 means that the UGen patched to TickRate will be ticked every time that TickRate is. Setting a rate of 0.5 means that the UGen patched to TickRate will be ticked at half the rate of TickRate (every other sample). Setting a rate of 2 means that the UGen patched to TickRate will be ticked twice every time that TickRate is ticked. The sample frame that TickRate generates can either be the same as the most recently generated sample frame from the UGen patched to it, or you can have it interpolate between that sample frame and the next sample frame from the UGen patched to it. At low tick rates, non-interpolated audio will sound like it is being bit-crushed. Essentially, this UGen allows you to control the sample rate of any UGen patched to it, with the limitation that you won’t be able to patch the output of that UGen anywhere else. That limitation is not enforced, but if you do so, your audio will not sound correct.
As for where to get the TickRate UGen, you can either copy the file from the Minim GitHub repo, or you can pull the repo and build the library locally.